Welcome to the $(r,c)$-graph database!
Maintained by: Yair Caro (University of Haifa-Oranim) and Xandru Mifsud (University of Malta)Introduction
This database concerns $(r, c)$-constant graphs (or simply $(r,c)$-graphs) which are $r$-regular graphs in which the subgraph induced by the open neighbourhood of every vertex has precisely $c$ edges. The family of $(r,c)$-graphs contains within it a large number of other families of important graphs, such as vertex-transitive graphs (and in particular Cayley graphs), graphs with constant link, $(r,b)$-regular graphs, strongly regular graphs, and more. The containment of these families is illustrated in the figure below.
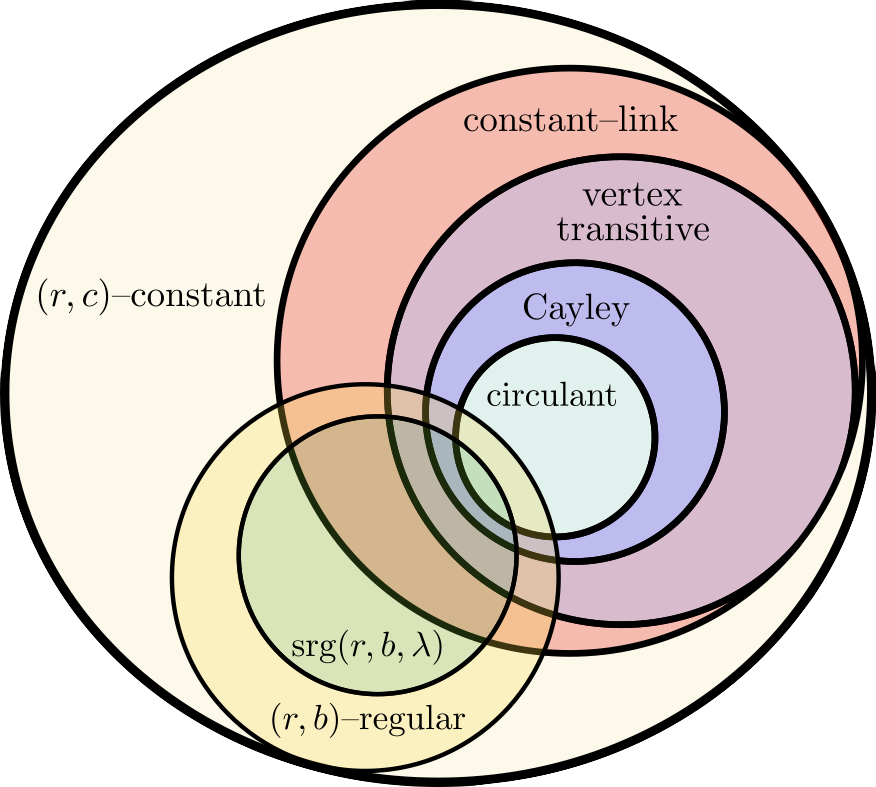
The family of $(r, c)$-graphs was recently introduced in [1], serving as an important tool in the construction of flip-graphs. We mention that an equivalent notion to $(r,c)$-graphs, with a focus and motivation on self-complementary graphs and strongly regular graphs, was introduced in [4] (after preliminary work in [3]) under the name `strongly vertex triangle regular graphs'.
The main facts concerning $(r,c)$-graphs in [1] are summarised below:
Fact 1 If $G$ and $H$ are, respectively, $(r_1, c_1)$ and $(r_2, c_2)$-graphs, then their Cartesian product $G \ \square \ H$ is an $(r_1 + r_2, c_1 + c_2)$-graph.
Fact 2 For $r \geq 1$ and $0 \leq c \leq \frac{r^2}{2} - 5r^{\frac{3}{2}}$, there exists an $(r,c)$-graph.
Fact 3 Furthermore, for $k \geq 1$ and $r \geq 3k$ there does not exist an $\left(r,\binom{r}{2} - k\right)$-graph.
Fact 4 Using Corollary 2.5 in [3] (and observing that $t(v)$ in the notation of [3] is $e(v)$ in our notation), it follows that if $G$ is an $(r,c)$-graph on $n$ vertices then the complement $\overline{G}$ is an $\left(n-1-r, \binom{n-1}{2} - \frac{3r(n-1-r)}{2} - c \right)$-graph.
Notes
(1) Data for $c = 0$ only includes non-bipartite and planar-bipartite graphs. Any $r$ regular bipartite graph is an $(r,0)$-graph.
(2) A number of data sources have been used for the compilation of this database, in conjunction with some code to check and generate $(r,c)$-graphs. In particular we make use of the GraphData repository in Mathematica [5], geng [6] and plantri [7].
Citations
Please cite as:[1] Y. Caro and X. Mifsud. "The $(r,c)$-graph database" (2024), Published online at: https://rcgraphs.research.um.edu.mt/
[2] Y. Caro and X. Mifsud, "On $(r,c)$-constant, planar and circulant graphs", Discussiones Mathematicae Graph Theory (2024), https://doi.org/10.7151/dmgt.2551